201211程序员下午真题
第 1 题
阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。
【说明】
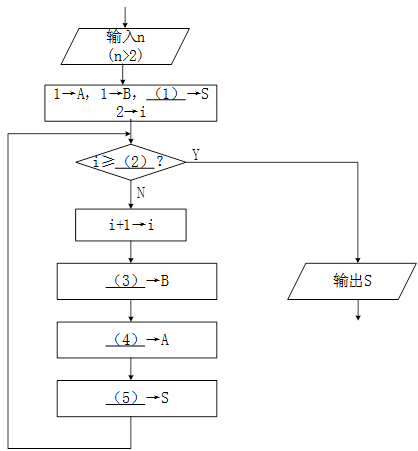
本流程图用于计算菲波那契数列 {a1=1,a2=1,…,an=an-1+an-2|n=3,4,…}的前n 项 ( n≥2) 之和 S。例如,菲波那契数列前6 项之和为 20。计算过程中,当前项之前的两项分别动态地保存在变量 A 和 B 中。
【流程图】
答案与解析
- 试题难度:较难
- 知识点:流程图>流程图
- 试题答案:(1)2或 A+B (2) n (3)A+B (4) B-A (5) S+B
- 试题解析:菲波那契数列的特点是首 2 项都是1,从第 3 项开始,每一项都是前两项之和。该数列的前几项为1, 1, 2 ,3,5,8,...。
在流程图中,送初始值 1→A ,1→B 后,显然前2项的和 S 应等于2,所以(1)处应填 2 (或 A+B) 。此时2→i (i 表示动态的项编号),说明已经计算出前2项之和。接着判断循环的结束条件。显然当1=n时表示已经计算出前 n 项之和,循环可以结束了。 因此(2)处填n。判断框中用">"或"≤"的效果是一样的,因为随着i的逐步增 1, 只要有 i=n结束条件,就不会遇到 i>n 的情况。不过编程的习惯使循环结束条件扩大些, 以防止逻辑出错时继续循环。
接下来 i+l →i 表示数列当前项的编号增1,继续往下计算。原来的前两项值(分别在变量 A 和 B 中)将变更成新的前两项再放到变量 A 和 B 中。

首先可以用 A+B→B 实现(原A) + (原B) →(新 B) ,因此(3)处填A+B 。为了填新 A 值(原来的B值),不能用 B→A,因为变量B的内容已经改变为(原A)+(原B) ,而B-A 正是((原A) + (原B)) - (原A) = (原B) ,因此可以用B-A→A 来实现新 A 的赋值。这样,(4) 处填 B-A 。最后应是前n项和值的累加(比原来的S值增加了新B值),所以 (5) 处应填S+B。填完各个空后,最好再用具体的数值来模拟流程图走几个循环检查所填的结果(这是防止逻辑上出错的好办法)。
第 2 题
阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。
【说明】
如果矩阵A中的元素A[i,j]满足条件: A[i,j]是第i行中值最小的元素,且又是第j列中值最大的元素,则称之为该矩阵的一个马鞍点。
一个矩阵可能存在多个马鞍点,也可能不存在马鞍点。下面的函数求解并输出一个矩阵中的所有马鞍点,最后返回该矩阵中马鞍点的个数。
【 C 函数】
int findSaddle(int a[] [N],int M)
{ / a 表示 M 行 N 列矩阵, N 是宏定义符号常量/
int row,column ,i,k;
int minElem;
int count = 0; / count 用于记录矩阵中马鞍点的个数/
for ( row = 0; row < (1) ; row++) {
/ minElem 用于表示第 row 行的最小元素值,其初值设为该行第 o 列的元素值/
(2)
for ( column = 1; column < (3) ; column++)
if ( minElem > a[row] [column] ){
minElem = a[row] [column);
}
for ( k = 0; k < N; k++ )
if ( a [row] [k] ==minElem ) {
/对第 row 行的每个最小元素,判断其是否为所在列的最大元素/
for (i = 0; i < M; i++)
if ( (4) > minElem ) break;
if (i>= (5) ) {
printf(" (%d ,%d): %d\n" ,row ,k ,minElem); /输出马鞍点/
count++;
}/if/
}/if/
}/for/
return count;
}/findSaddle/
答案与解析
- 试题难度:较难
- 知识点:C程序设计>C程序设计
- 试题答案:(1)M
(2)minElem = a[row][0] 或其等价形式
(3)N
(4)a[i][k]或其等价形式
(5) M - 试题解析:本题考查C程序设计基本技术。题目中涉及的主要知识点为二维数组和程序控制逻辑。首先应认真阅读题目的说明部分,以了解函数代码的功能和大致的处理思路,然后理清代码的框架,明确各个变量(或数组元素)所起的作用,并以语句组分析各段代码的功能,从而完成空缺处的代码填充。
由于矩阵中的马鞍点 A[i,j]是其所在行的最小元素,同时又是其所在列的最大元素,因此,对于矩阵中的每一行元素,先找出其最小者之值(用minElem 表示),然后判断每一行的最小元素是否为其所在列的最大元素,若是则找到了一个马鞍点。
显然,空(1)所在的表达式用于判断 M 行 N 列矩阵中的行数,因此应填入“M”。
空(2)处应对变量minElem设置初始值。根据注释,minElem 用于表示第row行的最小元素值,其初值设为该行第0列的元素值,因此空(2)处应填入 “minElem = a[row][0]”。
空(3)所在的 for 语句用于找出一行中的最小元素,column 应索引至每行的最后一个元素,因此空(3)处应填入“N”。
找出一行中的最小元素后,还要判断该元素是否为其所在列的最大元素。由于可能存在多个马鞍点,因此,一行中的最小元素可能不唯一,所以需要重新扫描该行的所有元素,一旦其等于最小元素值,则有可能成为马鞍点。实现该功能的代码如下:
for ( k = 0; k < N; k++ )
if ( a[row] [k]==minElem ) {
/对第 row 行的每个最小元素,判断其是否为所在列的最大元素/
for (i=0; i < M; i++)
if ( (4) > minElem ) break;
if ( i>= (5) ){
printf(" (%d ,%d) : %d\n" ,row ,k ,minElem); /输出马鞍点/
count++;
}/if/
}/if/
由于k的取值范围为[0,N],且k作为元素a[row][k]的列下标(或第二下标),因此当 “a[row][k]=minElem”时,即在第row行上找到了一个最小元素 a[row][k],接下来就判断它是否为所在列的最大元素了,空(4)所在的语句“for (i=0;i<M;i++)”实现该判断处理。若空(4)处所在的表达式为真,则通过break 跳出i作为循环控制的for语句。显然,根据该表达式的作用,当元素a[i][k]大于minElem 时 (minElem 与a[row][k]相等),说明a[row][k]虽然是其所在行的最小元素,但它不是其所在列(第k列)的最大元素,因此,可确定 a[row][k]不是马鞍点。
当然,如果在第k列上没有找到比 a(row][k]更大的元素,则 a[row][k]即是马鞍点。 结合空(4),可知空(5)应填入 "M"。
第 3 题
阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。
【说明】
函数Insert_key(root ,key)的功能是将键值 key 插入到boot指向根结点的二叉查找树中(二叉查找树为空时 *root 为空指针)。若给定的二叉查找树中已经包含键值为 key 的结点,则不进行插入操作井返回 0;否则申请新结点、存入 key 的值并将新结点加入树中,返回1。
提示:
- 二叉查找树又称为二叉排序树,它或者是一棵空树,或者是具有如下性质的二叉树:
- 若它的左子树非空,则其左子树上所有结点的键值均小于根结点的键值;
- 若它的右子树非空,则其右子树上所有结点的键值均大于根结点的键值;
- 左、右子树本身就是二叉查找树。
Typedef struct BiTnode{
int key_value; /结点的键值,为非负整数/
Struct BiTnodeleft,right; /结点的左、右子树指针/
}BiTnode,*BSTree;
【C 函数】
int Insert_key ( BSTree root ,int key )
{
BiTnode father = NULL ,p = root ,s;
while ((1)&& key != p->key_value ) { /查找键值为key的结点/
father = p;
if ( key < p->key_value) p =(2); /进入左子树/
else p =(3); /进入右子树/
}
if (p) return 0; /二叉查找树中己存在键值为 key 的结点,无需再插入/
s = (BiTnode )malloc ((4)); /根据结点类型生成新结点/
if (!s) return -1;
s->key_value = key; s->left = NULL; s->right = NULL;
if ( !father )
(5); /新结点作为二叉查找树的根结点/
else /新结点插入二叉查找树的适当位置/
if ( key < father->key_value) father->left = s;
else father->right = s;
return 1;
}
答案与解析
- 试题难度:较难
- 知识点:C程序设计>C程序设计
- 试题答案:(1) p 或 p!=NULL
(2) p->left或father->left
(3) p->right或father->right
(4) sizeof(BiTnode)
(5) *root = s - 试题解析:本题考查 C 程序设计基本技术及指针的应用。
题目中涉及的考点主要有链表的查找、插入运算以及程序逻辑,分析程序时首先要明确各个变量所起的作用,并按照、语句组分析各段代码的功能,从而完成空缺处的代码填充。
在二叉排序树上插入结点时,首先应通过查找运算确定结点的插入位置。空(1)~(3)所在代码段即用来实现二叉排序树的查找运算。
根据说明,指针变量 p 的初始值设置为指向根结点 (p = root) ,在通过指针访问链表中的结点时,应确保 p 的值为非空指针才行,因此空(2)处应填入 "p" 或 "p!=NULL"。 若待查找的键值 key 等于p指向结点的键值 key_value ,则查找成功且p 正指向所找到的 结点:若 key<p->key_value ,则应令p指向左子树结点,即空(2)处应填入"p->left" 否则令p指向右子树结点,即空(3)处应填入"p-〉right",从而根据待查找键值的大小进入了结点的子树。
空(4)所在代码生成待插入键值所需结点,根据链表结点类型的定义,此处应填
入"sizeof(BiTnode)"。
空(5)所在语句处理将新结点作为二叉查找树的根结点的情况,根据参数root的作用,此处应填入" root = s"。
第 4 题
阅读以下说明和 C 函数,填充函数中的空缺,将解答填入答题纸的对应栏内。
【说明】
己知两个整数数组 A 和 B 中分别存放了长度为 m 和 n 的两个非递减有序序列,函数 Adjustment(A,B,m,n)的功能是合并两个非递减序列,并将序列的前m个整数存入A中,其余元素依序存入 B 中。
例如:
合并过程如下:从数组 A 的第一个元素开始处理。用数组 B 的最小元素 B[0]与数组 A 的当前元素比较,若 A 的元素较小,则继续考查 A 的下一个元素;否则,先将A的最大元素暂存入temp ,然后移动A中的元素挪出空闲单元并将 B[0]插入数组 A ,最后将暂存在temp 中的数据插入数组B的适当位置(保持 B的有序性)。如此重复,直到A中所有元素都不大于B中所有元素为止。
【C 函数】
void Adjustment(int A[] ,int B[] ,int m ,int n)
{ /数组 A 有 m 个元素,数组 B 有 n 个元素/
int i ,k ,temp;
for(i = 0; i < m; i++)
{
if (A[i] <= B[0]) continue;
temp =(1); /将 A 中的最大元素备份至 temp /
/从后往前依次考查 A 的元素,移动 A 的元素并将来自 B 的最小元素插入 A 中/
for(k = m-1; (2); k--)
A[k] = A[k-1];
A[i] =(3);
/将备份在 temp 的数据插入数组 B 的适当位置/
for(k = 1;(4)&& k < n; k++)
B[k-1] = B[k];
B[k-1] =(5);
}
}
答案与解析
- 试题难度:较难
- 知识点:C程序设计>C程序设计
- 试题答案:(1) A[m-1,或(A+m-1),或其等价表示
(2) k>i ,或其等价表示
(3) B[0] ,或B
(4) temp> B[k],或 temp> *(B+k) ,或其等价表示
(5) temp - 试题解析:本题考查 C 程序设计基本技术。
题目中涉及的考点主要有一维数组及程序的运算逻辑,分析代码时首先要明确各个变量所起的作用,并按照语句组分析各段代码的功能,从而完成空缺处的代码。
根据题目中的说明和注释,此题的代码逻辑较为清楚。显然,A 的最大元素总是其
最后一个元素,因此,空(1)处应填入"A[m-1]"。
空(2)所在语句从后往前移动A的元素,然后将来自B的最小元素插入A 数组的适当位置,显然需要通过比较 B[0]与A中的元素来查找插入位置。
对于 B[0]与A中的元素的比较处理,其对应的语句如下:
for(i=0;i<m;i++)
{
if(A[i]<=B[0]) continue;
...
}
该语句的作用是将i的值增加到 A[i] >B[0]时为止,即 B[0]是正好小于 A[i]且最接近 A[i]的元素时i的值。
因此,空(2)处应填入 "k〉i" ,使得其所在的for语句能完成将大于或等于 B[0]的元素向后移动(A[k]= A[k-1]) ,接下来在空(3)处将元素 B[0]的值放入A[i],即空(3)处应填入 "B[0]"。
最后需要将备份在temp的数据插入数组B的适当位置。由于原来保存在B[0]中的值已插入A中,因此 B[0]目前是一个空闲单元,如果temp的值比B[1]、B[2]等元素都要大,则需要将B[1]、B[2]等元素的值依次前移,因此空(4)处应填入"temp > B[k] "。完成元素的移动后,将暂存于temp中的元素放入B的适当位置,即空(5)处应填入"temp" 。
第 5 题
阅读以下说明和c++代码,填充代码中的空缺,将解答填入答题纸的对应栏内。
【说明】
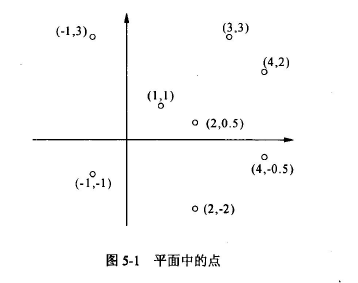
下面的程序用来计算并寻找平面坐标系中给定点中最近的点对(若存在多对,则输出其中的一对即可)。程序运行时,先输入点的个数和一组互异的点的坐标,通过计算每对点之间的距离,从而确定出距离最近的点对。例如,在图 5-1 所示的8个点中,点(1,1) 与(2,0.5)是间距最近的点对。
【C++代码】
include <iostream>
include <cmath>
using namespace std;
class GPoint {
private:
double x ,y;
public:
void setX(double x) { this->x = x; }
void setY(double y) { this->y = y; }
double getX() { return this->x; }
double getY() { return this->y; }
}
class ComputeDistance {
public:
double distance(GPoint a ,GPoint b) {
return sqrt((a.getX() - b.getX())(a .getX() - b.getX())
+ (a.getY() - b.getY())(a.getY() - b.getY()));
}
};
int main ()
{
int i ,j ,numberOfPoints = 0;
cout << "输入点的个数:";
cin >> numberOfpoints;
(1)points = new GPoint[numberOfPoints]; //创建保存点坐标的数组
memset(points ,0 ,sizeof(points));
cout << "输入" << numberOfPoints<< "个点的坐标 :";
for (i = 0; i < numberOfPoints; i++) {
double tmpx ,tmpy;
cin>>tmpx>>tmpy;
points[i] .setX(tmpx);
points[i] .setY(tmpy);
}
(2)computeDistance = new ComputeDistance();
int p1 = 0 ,p2=1; //p1 和 p2 用于表示距离最近的点对在数组中的下标
double shortestDistance = computeDistance->distance(points[p1] ,points[p2]);
//计算每一对点之间的距离
for (i = 0; i < numberOfPoints; i++) {
for (j = i+1; j <(3); j++) {
double tmpDistance = computeDistance->(4);
if ( (5) ) {
p1 = i; p2 = j;
shortestDistance = tmpDistance;
}
}
}
cout << "距离最近的点对是: (" ;
cout << points[p1] .getX() << "," << points[pl] .gety()<<")和(" ;
cout << points [p2].getX () << "," << points [p2].gety () << ")" << endl;
delete computeDistance;
return 0;
}
答案与解析
- 试题难度:较难
- 知识点:C++程序设计>C++程序设计
- 试题答案:(1)GPoint
(2)ComputeDistance
(3)numberOfPoints
(4)distance(points[i],points[j])
(5)shortestDistance > tmpDistance - 试题解析:本题考查 C++语言程序设计的能力,涉及类、对象、函数的定义和相关操作。要求考生根据给出的案例和执行过程说明,认真阅读理清程序思路,然后完成题目。
先考察题目说明。计算平面或空间中点之间的距离是目前很多应用中需要的,如 GPS 计算等。本题目简化了点之间距离的要求,其主要任务是计算井寻找平面坐标系中给定点中最近的点对(若存在多对,则输出其中的一对即可)。数轴上两点之间的距离等于相应两数差的绝对值,而平面坐标系中两点之间的距离等于相应两点的横坐标差和纵坐标差的平方和的算数平方根。假设平面左边系中的两点P1(X1,Yl)和P2(X2 ,Y2) ,两者之间的距离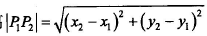
如题中图 5-1 所示的 8 个点中,点 (1,1)和(2,0.5) 之间的距离为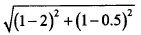
根据说明,点是一种类型,设计为类GPoint,点之间的距离设计为类ComputeDistance ,整体主逻辑代码在main函数中实现。类设计时,一般将属性设置为private,而对其的获取和更改等操作通过其中public方法进行。因此,在GPoint设计时,将x和y坐标设计为 private属性,将读取和设置 x 和 y 坐标的值设计为相应的get和set函数;在设计点之间的距离类ComputeDistance时,将两个 GPoint类的对象作为distance函数的参数传递。
main函数中实现控制流程,在程序运行时,先输入点的个数,创建相应大小的数组,再输入相应个数的一组互异的点的坐标,将点保存在一个数组中。C++中定义指向对象数组的指针的创建方式为
ClassName varName = new ClassName[numberOfArray];
用new创建对象数据返回的是指针类型,此处需要ClassName。然后在对数组内存空间清零之后,输入相应个数的互异的点的坐标,存入点数组,然后通过计算每对点之间的距离,从而确定距离最近的点对。其计算方式是:预设定第一次参与运算的两个点之间的距离为最短距离,然后计算每一对点之间的距离,其计算过程为从第一个点开始依次和其后所有的点之间调用两点之间距离计算函数计算其他点之间距离,每次计算和设定的最短距离进行比较,如果比当前最短距离短,则更新最短距离并记录相应的点。最后输出所记录的最短距离和相应的点。
因此,空(1)需要指向 GPoint 类型的对象数组的指针,即为 GPoint;空(2)需要计算两点之间距离的对象,用new创建,所以 ComputeDistance ;空(3)处判定是否所有与当前点还没有比较过的点之间的距离都计算完成,因为当前点和在数组前面的点的比较在前面计算时已经计算过,所以从和后一个点计算直到数组的最后一个点计算完成,即j<numberOfPoints,即空(3)为numberOfPoints; 空(4)处调用computeDistance的distance函数,计算当前循环的两个点之间的距离,即 distance(points[i],points [j]);空(5)处通过判定计算出的当前两个点之间的距离和当前最短距离,来判定是否需要更新当前最短距离,即 shortestDistance > tmpDistance 。
第 6 题
阅读以下说明和 Java 程序,填充程序中的空缺,将解答填入答题纸的对应栏内。
【说明】
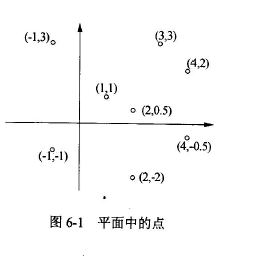
下面的程序用来计算并寻找平面坐标系中给定点中最近的点对(若存在多对,则输出其中的一对即可)。程序运行时,先输入点的个数和一组互异的点的坐标,通过计算每对点之间的距离,从而确定出距离最近的点对。例如,在图6-1所示的8个点中,点(1,1)与(2,0.5)是间距最近的点对。
【Java代码】
import java.util.Scanner;
class GPoint
{
private double x ,y;
public void setX(double x) { this.x = x; }
public void setY(double y) { this.y = y; }
public double getX( ) { return this.x; }
public double getY() { return this.y; }
}
class FindNearestPoints {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print(" 输入点的个数: ");
int numberOfPoints = input.nextInt( );
(1)points = new GPoint[numberOfPoints); //创建保存点坐标
的数组
System.out.print("请输入" + numberOfPoints + "个点的坐标: ");
for (int i = 0; i < points.length; i++) {
points [i] = (2);
points[i].setX(input.nextDouble( ));
points[i].setY(input.nextDouble( ));
}
FindNearestPoints fnp = new FindNearestPoints( );
int p1 = 0 ,p2 = 1; / / p1 和 p2 用于表示距离最近的点对在数组中的下标
double shortestDistance= fnp.getDistance (points [p1],points[p2]);
//计算每一对点之间的距离
for (int i = 0; i < points.length; i++)
{
for (int j = i + 1; j < (3); j++)
{
double tmpDistance = fnp.(4)
//计算两点间的距离
if ( (5))
{
p1= i;
p2 = j;
shortestDistance = tmpDistance;
}
}
}
System.out.println(" 距离最近的点对是(" +
points[p1].getX( ) + "," + points[p1].gety( ) + ")和(" +
points[p2] .getX( ) + ", " + points[p2] .gety( ) + ")");
}
public double getDistance(GPoint pt1,GPoint pt2)
{
return Math. sqrt ((pt2.getX ( ) - pt1.getX ( )) (pt2.getX ( ) -pt1.getX ( ))
+ (pt2.gety( ) - pt1.getY( )) (pt2.getY( ) - pt1.getY( )));
}
}
答案与解析
- 试题难度:较难
- 知识点:Java程序设计>Java程序设计案例
- 试题答案:(1) GPoint[]
(2) new GPoint()
(3) points .length 或 numberOfPoints
(4) getDistance(points[i],points [j])
(5) shortestDistance >tmpDistance - 试题解析:本题考查 Java 语言程序设计的能力,涉及类、对象、方法的定义和相关操作。要求考生根据给出的案例和执行过程说明,认真阅读理清程序思路,然后完成题目。
先考察题目说明。计算平面或空间中点之间的距离是目前很多应用中需要的,如GPS计算等。本题目简化了点之间距离的要求,其主要任务是计算并寻找平面坐标系中给定点中最近的点对(若存在多对,则输出其中的一对即可)。数轴上两点之间的距离等于相应两数差的绝对值,而平面坐标系中两点之间的距离等于相应两点的横坐标差和纵坐标差的平方和的算数平方根。假设平面左边系中的两点P1(X1,Yl)和P2(X2 ,Y2) ,两者之间的距离
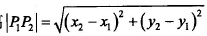
如题中图6-1 所示的8个点中,点 (1,1) 和 (2,0.5) 之间的距离为
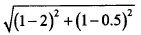
根据说明,点是一种类型,设计为类GPoint;寻找点之间的距离设计为FindNearestPoints ,整体主逻辑代码在其中的main方法中实现。类设计时,一般将属性 设置为private ,而对其的获取和更改等操作通过其中public方法进行。因此,在GPoint 设计时,将x和y坐标设计为private属性,将读取和设置x和y坐标的值设计相应的get 和set方法:在设计寻找距离最近的点的类 FindNearestPoints 时,其主要方法包括计算两个点之间的距离方法getDistance ,将两GPoint类的对象作为 distance方法的参数传递。
FindNearestPoints中的main方法执行控制流程,在程序运行时,先输入点的个数,创建相应大小的数组,再输入相应个数的一组互异的点的坐标,将点保存在一个数组 points中。Java中对象数组的创建方式为:
ClassName[] varName = new ClassName[numberOfArray];
或者:
ClassName varName[] = new ClassName[numbe rOfArray];
然后输入相应个数的互异的点的坐标,存入点数组,然后通过计算每对点之间的距离,从而确定出距离最近的点对。其计算方式是:预设定第一次参与运算的两个点之间的距离为最短距离,然后计算每一对点之间的距离,其计算过程为从第一个点开始依次和其后所有的点之间调用两点之间距离计算函数计算其他点之间距离,每次计算和设定的最短距离进行比较,如果比当前最短距离短,则更新最短距离并记录相应的点。最后输出所记录的最短距离和相应的点。
因此空(1)需要声明GPoint类型的对象数组,即为GPoint[]; 空(2)需要对数组中的每个对象进行初始化,即new GPoint(); 空(3)处判定是否所有与当前点还没有比较过的点之间的距离都计算完成,因为当前点和在数组前面的点的比较在前面计算时已经计算过,所以从和后一个点计算直到数组的最后一个点计算完成,即j<points.length,即空(3)为 points.length;空(4)处调用 getDistance 方法,计算当前循环的两个点之间的距离,即 getDistance(points[i],points[j]);空(5)处通过判定计算出的当前两个点之间的距离和当前最短距离,来判定是否需要更新当前最短距离,即shortestDistance>tmpDistance 。